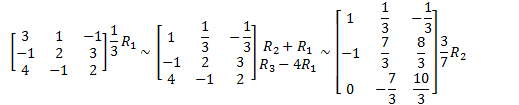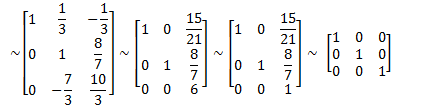Lec 9 - Echelon Reduce Operations
Monday, January 23, 2012
9:29 AM
- All rows that have at least non-zero entry are above rows with only zeros.
- The leftmost non-zero entry in a row is a 1, called a leading one.
- The leading one in a row is to the right of the leading one in any row above it.
- Any column containing a leading one has it as its only non-zero entry.
Recall:
A matrix is in reduced row echelon form (RREF) if:
(Note: Every Matrix has a UNIQUE RREF)
Eg
Solve
![]()
![]()
![]()
![]()

![]()
Represents
![]()
![]()
![]()
Solution is:
![]()
Eg
Solve
![]()
![]()
![]()
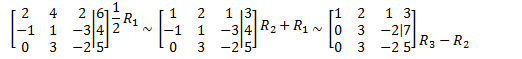
![]()
![]()
Since there is no choice of variables, this system is inconsistent.
![]()
Eg
Solve


![]()
Represents:
![]()
![]()
![]()
![]()
![]()
![]()
The solution set of the system is
![]()
![]()
![]()
Definition:
![]()
![]()
Eg
Solve
![]()
![]()
![]()

Let
![]()
![]()
![]()
![]()
![]()
The solution set is

![]()
Eg
![]()
We must solve the system
![]()
![]()
![]()
![]()
![]() Homogeneous
Systems
Homogeneous
Systems
Definition
A system of linear equations is homogeneous if the RHS contains only zeros.
![]()
![]()
Note: Performing ERPs on a homogeneous system will not change the RHS. We just perform EROs on the coefficient matrix.
Eg
Solve
![]()
![]()
![]()